Presentación:
Nuestro
grupo; conformado por Alejandro Aguilar, Ricardo Gonzales, Giancarlo Núñez y
Juan Carlos Torpoco; va a llevar a cabo este proyecto cuyo objetivo será medir
la altura de un edificio mostrando los cálculos paso a paso.
El
motivo de este proyecto, Calculando alturas con el goniómetro casero, es medir
edificios grandes de una manera simple sin la necesidad de mucho trabajo. Con
este proyecto aprenderemos cómo podemos calcular alturas con simples materiales
caseros. Solo necesitamos un transportador, cinta adhesiva, medio metro de
pabilo y un llavero o cualquier otro objeto con peso significativo.
Este
trabajo consiste de un video, una presentación en el programa Power Point, un
video donde se muestre tanto la creación del goniómetro como su uso y un blog
donde adjuntemos todo el trabajo pero, la creación de este último es opcional.
También anexaremos la hoja de trabajo con la que hicimos la parte del proyecto
dentro del colegio, donde se muestra cómo medimos un edificio de manera simple,
sencilla y rápida.
En
este caso mediremos el supermercado Plaza Vea del Molina Plaza ubicado en la
av. Raúl Ferrero. Todo nuestro proceso será grabado, desde la creación del
goniómetro, hasta los cálculos de la altura con los datos que obtendremos.
Fundamentación teórica:
La
goniometría, del griego γωνία' (gonía: ángulo) y μέτϿον (métron: medida),
es la ciencia y técnica de medición de ángulos, de su construcción y su
trazado. Por extensión abarca todo lo que es trigonometría analítica, o sea; el
estudio de razones trigonométricas.
Existen
varios instrumentos de medición utilizados con distintos propósitos, como por
ejemplo, en la navegación marítima, este instrumento, el goniómetro, reemplazó
al astrolabio debido a su mayor precisión. Otros instrumentos de medición, como
el giroteodolito, son usados en cosas sencillas como la orientación del norte
verdadero mediante la locación de los meridianos como en la industria de la
minería subterránea y en la ingeniería de túneles, donde es considerado el
instrumento principal.
El
goniómetro, también llamado transportador universal, es un instrumento de
medición con forma semicircular, graduado en 180° y es utilizado para medir o
construir ángulos, comprobación de conos y puesta a punto de las máquinas o
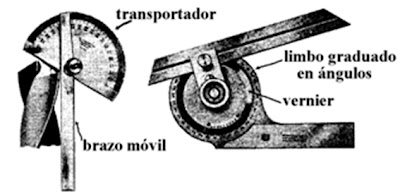
herramientas de los talleres de mecanizado. El más sencillo (imagen de la izquierda)
consta de un semicírculo graduado, transportador, y un brazo móvil. El
goniómetro universal (imagen de la derecha) está formado por dos reglas, uno
con un limbo graduado en ángulos y la otra con un vernier circular y un anillo
para que gire el limbo de la otra regla. Ambas reglas poseen un tornillo de
fijación que los inmoviliza pero deja que giren.
Los
usos de la goniometría son varios. En la astronomía, el ángulo formado por dos
visuales tangentes a los bordes opuestos de un planeta o de una galaxia para
poder calcular su diámetro. En el ángulo de se funda en la formación de los
ángulos. En la geodesia ya que son la
triangulación de territorios, representa un papel importante en la medición
angular. Es por eso que se usa el goniómetro. En la mineralogía se usa un
goniómetro de reflexión en el cual un cristal es fijado en el centro de un
círculo graduado en el cual giran dispuestos radialmente y así se forma un
ángulo de reflexión que deduce el valor de los ángulos diedros formados por la
cara del cristal. En la medicina este artefacto se usa para medir el ángulo de
movilidad articular de lesiones, principalmente. Finalmente, en la biomecánica,
se usa el goniómetro para medir la movilidad de la persona que presenta cuando
ejecuta alguna técnica deportiva. De hecho, al usar la goniometría en este tipo
de casos, resulta un mayor interés.
Experiencia en campo:
Como
habíamos dicho anteriormente, vamos a medir el edificio del supermercado Plaza
Vea, ubicado en Molina Plaza.
Primero,
vamos a hacer un gráfico para representar lo que hemos hecho.
Luego,
vamos a poner nuestros datos que hemos conseguido por el goniómetro.
Sabiendo
que h = 1,615 m d = 3,75 m α = 20°
β = 25° x = ? H = ?
Ahora,
para hallar “H” necesitamos hallar “x”. Para ello, hay que plantear dos
ecuaciones:
tg(α) = H – h
d
+ x
H = (d + x)tg(α) + h
|
tg(β) = H – h
x
H = xtg(β) + h
|
Y de
ahí resolvámosla.
(d + x)tg(α) + h = xtg(β) + h
xtg(β) – xtg(α) = dtg(α)
x(tg(β) – tg(α)) = dtg(α)
x(tg(β) – tg(α)) = dtg(α)
x(tg(25°) – tg(20°)) = (3,75)tg(20°)
x(0,466 – 0,364) = (3,75)(0,364)
0,102x = 1,365
x =
13,38 m
Ahora,
solo nos faltaría hallar la altura del edificio; es decir, H.
tg(β) = H – h
x
H = xtg(β) + h
H =
(13,38)(0,466) + h
H = 6,23 + 1,615
H = 7,85 m
Por
lo tanto, la altura del edificio mide 7,85 m.
Para
más información visite nuestro vídeo; lo puede ver en la siguiente página:
Conclusiones:
Ø La
primera conclusión básica, sacada de la experiencia de campo, es que a menor
distancia mayor ángulo.
Ø La
segunda conclusión es que no existe la necesidad de acercarnos a medir la
distancia entre el edificio que queremos medir y nuestro punto de medición.
Basta con establecer dos puntos distintos con una distancia relativamente
mediana, con la distancia desde el edificio, para sacar la altura de este.
Ø La
tercera conclusión es que no hay necesidad de distintos y complejos materiales
como los que usaron los antiguos matemáticos y usan algunos ingenieros civiles
en la actualidad, basta el ingenio para hacer grandes cosas.
Ø Edificios,
montañas, puentes, torres y otras cosas más grandes todavía que antes del
proyecto pensábamos que no podríamos medirlas, y si es que lo hubiéramos hecho
nos hubiera tomado mucho más trabajo, sus medidas accesibles a nuestro estudio.
Anexos:
Por último podrán ver nuestro trabajo en otro formato y/o una continuación.
Proyecto calculando alturas - YouTube:
Para ver este vídeo desde el sitio web vayan a esta dirección:
Traba escrito - Slideshare:
Para descargar este trabajo escrito en Word vayan a esta dirección:
http://www.slideshare.net/RuickGV/proyecto-calculando-alturas-12763247/download
http://www.slideshare.net/RuickGV/proyecto-calculando-alturas-12763247/download
Ejemplo de aplicación- Slideshare:
Para descargar este PDF vayan a esta dirección:
Power Point - Slideshare:
Bibliografía:
Ø Clases
didácticas del profesor Luis Dávila, en el colegio San Pedro.
Ø Wikipedia.